电磁学乱七八糟的符号(三)
这里重点是针对各种入射反射折射,chapter5 电磁波的传播
[TOC]
review
1.上两张图说明一下极化是怎么回事
2.行波与驻波
1.驻波
每一个点都在等相位震荡
借了,平面电磁波,理想介质to理想导体,垂直入射 讲了一下
2.行波(没找到好一点的图,凑合着看吧)
每一个点都在等幅震荡
平面电磁波,理想介质to理想介质,垂直入射
这里借一个最普通的情况,说明基本概念:
反射系数R
$$ R=\frac {E^{-r}{x0}}{E^{+i}{x0}}=\frac{\eta_2-\eta_1}{\eta2+\eta1}$$
定义为边界上反射波电场分量与入射波电场分量之比
折射系数T
$$ T=\frac {E^{+t}{x0}}{E^{+i}{x0}}=\frac{2\eta_2}{\eta2+\eta1}$$
定义为边界上折射波电场分量与入射波电场分量之比
可以观察到有:
$$T-R=1$$
###合成波场量
看书的图看书的图看书的图看书的图:
$$ E_{1x}(z)= E^{+i}{xo}(1-R)e^{-jk{1}z}+2RE^{+i}{x0}cosk{1}z $$
$$H_{1y}(z)=\frac{E^{+i}{x0}}{\eta_1}(1-R)e^{jk{1}z}+2R\frac{E^{+i}{x0}}{\eta_1}e^{-j\frac{\pi}{2}}sink_1z$$
对于折射波:
$$E{2x}(z)=TE^{+i}{x0}e^{-jk_2 z}$$
$$E{2y}(z)=T\frac{E^{+i}_{x0}}{\eta_2}e^{-jk_2 z}$$
平面电磁波,理想介质to理想介质,斜入射
1.垂直极化波
1.垂直极化波:电场强度分量与入射角垂直的波称为垂直极化波
斯涅尔反射定律
$$ \theta_i=\theta_r $$
斯涅尔折射定律
$$ \frac {sin \theta_i}{sin \theta_t}=\frac{k_2}{k_1}=\frac{n_2}{n_1} $$
其中
折射指数,折射率
$$ n=c\sqrt{\mu\varepsilon}=\frac c \omega k $$
垂直极化波的反射系数和折射系数
$$R_{\bot}=\frac{\eta_{2}cos\theta_{i}-{\eta_{1}cos\theta_{t}}}{\eta_{2}cos\theta_{i}+{\eta_{1}cos\theta_{t}}}$$
$$T_{\bot}=\frac{2\eta_{2}cos\theta_{i}}{\eta_{2}cos\theta_{i}+{\eta_{1}cos\theta_{t}}}$$
对于非铁磁性媒质,$\mu_{1}\approx\mu_{2}\approx\mu_{0}$,则有$\frac{\eta_{1}}{\eta_{2}}=\sqrt{\frac{\varepsilon_{1}}{\varepsilon_{2}}}$和$sin\theta_{t}=\sqrt{\frac{\varepsilon_{2}}{\varepsilon_{1}}}$上式可改为
$$R_{\bot}=\frac{cos\theta_{i}-\sqrt{\frac{\epsilon_{2}}{\epsilon_{1}}-sin^{2}\theta_{i}}}{cos\theta_{i}+\sqrt{\frac{\epsilon_{2}}{\epsilon_{1}}-sin^{2}\theta_{i}}}$$
$$T_{\bot}=\frac{2cos\theta_{i}}{cos\theta_{i}+\sqrt{\frac{\epsilon_{2}}{\epsilon_{1}}-sin^{2}\theta_{i}}}$$
平行极化波
平行极化波:电场强度分量与入射角平行的波称为平行极化波
平行极化波的发射系数和折射系数:
$$R_{//}=\frac{\eta_{1}cos\theta_{i}-{\eta_{2}cos\theta_{t}}}{\eta_{1}cos\theta_{i}+{\eta_{2}cos\theta_{t}}}$$
$$T_{//}=\frac{2\eta_{2}cos\theta_{i}}{\eta_{1}cos\theta_{i}+{\eta_{2}cos\theta_{t}}}$$
对于非铁磁性媒介,上两式可改写为
$$R_{//}=\frac{({\varepsilon_{2}/\varepsilon_{1}})cos\theta_{i}-\sqrt{\frac{\epsilon_{2}}{\epsilon_{1}}-sin^{2}\theta_{i}}}{({\varepsilon_{2}/\varepsilon_{1}})cos\theta_{i}+\sqrt{\frac{\epsilon_{2}}{\epsilon_{1}}-sin^{2}\theta_{i}}}$$
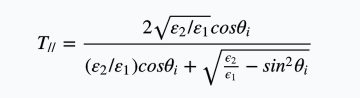
公式太长被识别为bug了,截图放之
显然,斜入射就是可以分解成垂直极化波和水平极化波而被介绍.
全反射
当 |R|=1时,入射波全部反射走了:
显然让$R_{\bot} $和$R_{//}$都等于1时会有全反射:
$$sin \theta_i =\sqrt{\frac {\varepsilon_2}{\varepsilon_1}} \tag {5,1}$$
对于非铁磁性媒质,$\mu_{1}\approx\mu_{2}\approx\mu_{0}$,有:
$$sin \theta_i =\sqrt{\frac {\varepsilon_2}{\varepsilon_1}}sin\theta_t$$
显然当$\theta_t=\frac \pi 2$时全反射,但这个不是重点,因为自变量是$\theta_i$,所以这只是一个现象而已.
所以有:
临界角$\theta_c$
满足1.1的$\theta_i$记作$\theta_c$有:
$$ \theta_c= arcsin \sqrt{\frac{\varepsilon_2}{\varepsilon_1}} $$
当$\theta_i =\theta_c 时有:sin\theta_c=1 ,\theta_t =\frac \pi 2$
全内反射
当入射角大于临界角之后,可以求出:
$$sin\theta_{3t}=\sqrt{\frac {\varepsilon_1}{\varepsilon_2}}sin\theta_{3i}>sin\theta_t=1$$
可以看出这个角用平面已经没办法解析了,应该放成复平面再用欧拉公式展开才能探看,但是所幸的是:
$$cos\theta_{3t} =\sqrt{1-sin^2\theta_{3t}}=\pm j \sqrt{\frac{\varepsilon_1}{\varepsilon_2}sin^2\theta_{3i}-1}\
\quad \quad=\pm j(\frac{\varepsilon_1}{\varepsilon_2})^{\frac 12}\sqrt{sin^2\theta_{3i}-\varepsilon_2/\varepsilon_1}=\pm j a$$
可以代入反射系数公式,还是可以得到$|R_{\bot}|=|R_{//}|=1$,还是达到了全反射的条件
但是这个时候,可以代入折射系数可知,$T_{\bot}\neq 0 , T_{//}\neq 0$,此时随便带入一个方向的折射波方程得(以垂直为例):
$$\vec E^t(\vec r)=\vec a_y T_{\bot}E^{+i}0 e^{-jk_2xsin\theta{3t}}e^{-jk_2zcos\theta_{3t}}\
\quad \vec a_y T_{\bot}E^{+i}0e^{-az}e^{jk_2 xsin\theta{3t}}$$
可以看到,此时的TEM波已经变成了
振幅往+z方向衰减,方向沿+x方向传播的非均匀平面波,综合反射折射来看,就可以说是很像光纤了
画了个小图,自己了解一下.
从图都可以得出,反射和折射的表面波之间是存在光程差,也就存在着相移,考虑该波等相面:
$$ k_2 xsin\theta_{3t}-\omega t=C $$
求导得相速:
慢波&&表面波
$$ v_{px} = \frac{\omega}{k_2 sin\theta_{3t}}=\frac {v_p}{sin\theta_{3t}}<v_p $$
所以称该波为慢波,或者是表面波
建议看书P147-148
4.全折射
同理,入射波全部折射进理想介质2,但理论上我们只考虑$R_{//}=0$具体原因可以看书!
整理得:
布儒斯特角&&极化角$\theta_b$
$$ sin \theta_i =\frac{\varepsilon_2}{\varepsilon_2 +\varepsilon_1} $$
当存在$\theta_i$满足上式时,记作布儒斯特角$\theta_b$:
$$\theta_b=arcsin\sqrt{\frac{\varepsilon_2}{\varepsilon_1+\varepsilon_2}}$$
此时会有垂直极化分量剩余,也就是说,发生全折射的时候,会剩下垂直极化分量
所以这过程也会被称为极化滤波.所以布儒斯特角也称为极化角
平面电磁波,理想介质to理想导体,垂直入射
由于良导体存在趋肤效应,所以研究折射是没有意义的,所以这里只需要研究全反射条件.
由前文的垂直入射的反射系数和折射系数可以看到:
$$ R=-1 \quad \quad T=0 $$
也可以由理想导体的边界中,电场强度切向连续得到,代入前面的垂直入射分析中得:
$$ \vec E_{1x}(z)=\vec E^{+i}{x0}(e^{-jk_1 z}-e^{jk_1 z}) = -j2\vec E^{+i}{x0}sink_1 z $$
$$ \vec E_{1y}(z)= \frac {\vec E^{+i}{x0}}{\eta_1} (e^{-jk_1 z}+e^{jk_1 z}) = \frac 2{\eta_1} \vec E^{+i}{x0}cosk_1 z $$
改写成瞬时形式:
$$ E_{1x}(z,t)=Re[E_{1x}(z)e^{j\omega t}]=2E^{+i}{x0} \quad \quad sink_1 z \quad \quad sin \omega t $$
$$ H{1y}(z,t)=Re[H_{1y}(z)e^{j\omega t}]=\frac 2 {\eta_1}E^{+i}_{x0}\quad \quad cosk_1 z\quad\quad cos\omega t $$
由公式可以看出:
- 在固定一个x-y平面(z固定),波幅只会因为t而改变,这个改变是通过改变相位而来的
- 在固定一个周期中(t固定), 相位不会因为z的传播而改变
- 在固定一个周期中(t固定), 波幅会因为z的传播而震荡
直观一点来说,只要你固定x-y平面,固定看一个周期,想着z往着图里投射波形,就可以看见blog开头的
纯驻波
还可以在时均能流密度$S_{av}$中:
$$ \vec S_{av}=\frac12 Re[\vec a_zE_{1x}(z)\vec H^*{1y}(z)] \
\quad \quad \quad \quad \quad \quad \quad \quad =\frac 12Re[-\vec a_z j\frac {4|E^{+i}{x0}|^2}{\eta_1}sink_1zcosk_1z]=0$$
可以看出驻波并不会传输能量,只是周期地把电场能量和磁场能量交换了而已.
平面电磁波,理想介质to理想导体,斜入射
跟之前是一样的,斜入射分成垂直极化波和水平极化波来分析
也是只研究全反射
垂直极化入射
垂直极化入射情况下的合成波:
$$\vec E_{1}(\vec r)=\vec E^{i}(\vec r)+\vec E^{r}(\vec r)\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\
= -\vec{a}{y}j2E^{+i}{0}\quad sin(k_{1}zcos\theta_{i})\quad e^{-jk_{1}xsin\theta_{i}}$$
$$\vec H_{1}(\vec r)=\vec H^{I}(\vec r)+\vec H^{r}(\vec r)\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \
\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad=[-\vec{a_{x}}cos\theta_{i}cos(k_{1}zcos\theta_{i})-\vec{a_{z}}jsin\theta_{i}sin(k_{1}zcos_{\theta_{i}})]\frac{2E^{+i}{0}}{\eta{1}}e^{-jk_{1}xsin\theta_{i}}$$
可以看出(统一看电场,因为几乎所有定义都是用电场定义的):
x方向上的行波性
由$e^{-j(k_{1}xsin\theta_{i}-\omega t)}$给出,而且传播相速为慢波:
$$ v_{px}=\frac{\omega}{k_1 sin\theta_i}=\frac{v_p}{sin \theta_i}<v_p $$
z方向上的驻波性
由$sin(k_{1}zcos\theta_{i})$可以得到
振幅非均匀性
振幅往+z方向做周期性变化,方向沿+x方向等相面 传播的非均匀平面波
以上者三点都有点类似于全内反射
横电波性(TE波)
平行极化入射
$$ \vec E_1(\vec r)=-[\vec a_x jcos\theta_i sin(k_1 zcos\theta_i)+\vec a_z sin\theta_i cos(k_1 zcos\theta_i)]
2E_0^{+i}e^{-jk_1 xsin\theta_i} $$
$$\vec H_1(\vec r)=\vec a_y 2\frac{E_0^{+i}}{\eta_1}cos(k_1 z cos\theta_i)e^{-jk_1 xcos\theta_i}$$
同上分析,依然有:
x方向上的行波性
行波因子$e^{-j(k_{1}xsin\theta_{i}-{\omega}t)}$
由行波因子表示,而且传播相速为慢波:
$$v_{px}=\frac{\omega}{k_1 sin\theta_i}=\frac{v_p}{sin \theta_i} < v_p$$
z方向上的驻波性
驻波因子$^{sin}{cos}(k{1}zcos\theta_{i})$
由驻波因子表示
振幅非均匀性
振幅随z变化的非均匀平面波
*横磁波(TM波)
在x的传播方向上电场分量不为0,磁场分量为0
结语
第五章算是写完了,剩下的内容课上也没有介绍了,也开始从单纯的抄写公式到以公式入手理解意义了.
但是万万不足的是,blog上大多其实还是结论,真正要处理的波动方程除了难一点的之外都没有写出,还需要大家好好看书!




